dahimatematik - Rasyonel Sayılar

Rasyonel sayılar genelde şöyle tanımlanır: $mathbb Q = { frac{a}{b} | a,b in mathbb Z and b neq 0 }$
(a ve b tam sayı ve sıfır olmamak üzere a/b şeklindeki sayılara Rasyonel sayı denir)

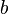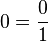$frac{2}{3}$ ve $frac{4}{6}$ veya $frac{6}{9}$ eşdeğer Rasyonel sayılardır. Dolayısıyla her Rasyonel sayı sonsuz şekilde ifade edilebilir. Rasyonel sayıların en basit formu $a!$ ve $b!$ tamsayılarının ortak böleninin olmadığı $a/b!$ ifadesidir. Her tam sayı Rasyonel sayıdır. Çünkü $-3=frac{-3}{1}$ veya $0=frac{0}{1}$ veya $43=frac{43}{1}$ şeklinde yani Rasyonel sayı tanımına uygun biçimde yazılabilirler.Rasyonel sayılar kümesi $mathbb{Q}$ , tam sayılar kümesi $mathbb{Z}$ 'yi kapsar. Yani $mathbb{Z} subset mathbb{Q}$ .Daha ince bir tanımı ise tam sayılar üzerinden tanımlanacak bir denklik bağıntısıyla yapılabilir. Böylece her denklik sınıfı bir Rasyonel sayı olarak anılır. $mathbb{Z} times mathbb{Z}$ kümesinden seçilmiş keyfî (a,b) ve (c,d) öğeleri için "~" bağıntısı $(a,b) sim (c,d) Leftrightarrow ad=bc, quad b,d not= 0$ olarak tanımlansın. Bunun bir denklik bağıntısı olduğu kolaylıkla kanıtlanabilir. Bu durumda, denklik sınıfları $overline{(a,b)} = {(a,b) | (a,b) sim (c,d) }$ olurlar. 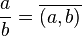Rasyonel sayı ise basitçe $frac{a}{b} = overline{(a,b)}$ şeklinde tanımlanır.Tanımda paydanın sıfır olmama şartı $frac{a}{0}$ ifadesinin tanımlanmamış olmasındandır. Bir sayının sıfıra bölümü tanımsızdır.Sıfırdan büyük olan rasyonel sayılara pozitif rasyonel sayılar, sıfırdan küçük rasyonel sayılar da negatif rasyonel sayılar denir.Pozitif rasyonel sayılar kümesi $mathbb Q^{+}$ ile gösterilir. Negatif rasyonel sayılar kümesi $mathbb Q^{-}$ ile gösterilir.

Örneğin

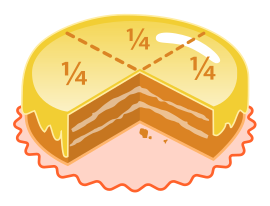
Dörde bölünüp, dörtte biri kesilip alınmış ve geri kalan dörtte üçü gösterilen bir yuvarlak pasta

Yandaki şekilde,bir bütün yuvarlak pasta 4 eş parçaya bölünmüş ve bu 4 eş parçalardan her birisi $frac{1}{4}$ olarak görülmektedir. Ancak bir parça alınmış olduğundan kalan eksikdir. Geriye kalan, dört eşit parçaya bölünmüş bütünün üç tane parçası (yani 3de 4 oranı) veya (kesiri)dir. Bu $frac{3}{4}$ ifadesi şeklinde gösterilir. Burada ifadede kesir çizgisinin üstündeki değere (yani 3e) pay, kesir çizgisinin altındaki değere (yani 4’e) payda denir. Bu kesir, “üç bölü dört” ya da “dörtte üç” diye okunur.

Konu başlıkları

[gizle]

1 Rasyonel sayıların cebirsel özellikleri
2 Rasyonel sayıların eşitliği
3 Rasyonel Sayıları Karşılaştırma (büyüklük ,küçüklük)
- 3.1 Payları eşit olan rasyonel sayılar

Rasyonel sayıların cebirsel özellikleri [düzenle]

$a, b, c, d in mathbb{Q}$ olmak üzere:

Rasyonel sayıların eşitliği [düzenle]

İki rasyonel sayının eşitliği, o sayıların pay ve paydalarının rasyonel olmasıyla anlaşılır. $a,b,c,d in mathbb{Z}$ olmak üzere $frac{a}{b}$ ve $frac{c}{d}$ iki rasyonel sayı ise bu iki sayı ancak $ad=bc!$ olduğunda eşittir.

Bu koşul, yukarıdaki tanımdan çıkarsanabilir. İki rasyonel sayı aynı denklik sınıfındaysa birbirine eşittir, Denklik bağıntısı da zaten $ad=bc!$ koşulunu içermekteydi.

Rasyonel Sayıları Karşılaştırma (büyüklük ,küçüklük) [düzenle]

Payları eşit olan rasyonel sayılar [düzenle]

Paydaları eşit olan rasyonel oranlar icin payı büyük olan daha büyük, payı küçük olan daha küçüktür.

Örneğin

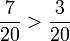
$frac{7}{20} > frac{3}{20}$

Burada paydalar eşit ve 20dir. Pay değerleri karşılaştırılınca soldaki pay 7 sagdaki pay 3 den daha büyük oldugu için, soldaki rasyonel oran daha büyüktür.

Unutmamalıdır ki negatif paylar karşılaştırılırken sadece mutlak değerlerin karşılaştırılması hatalı olup negatif işaretlerinin de ele alınması ve negatif sayılı pay değerlerde mutlak değeri büyük görünen sayının daha küçük olduğu hatırlanmalıdır:

Payda 20ye eşit olup sağda ki negatif pay değeri -3, sağdaki negatif pay değeri olan -7den daha büyük olduğu için sağdaki oran daha büyüktür.